ABORIGINAL AND TORRES STRAIT ISLANDER
HEALTH PERFORMANCE FRAMEWORK 2017 REPORT

Aboriginal and Torres Strait Islander peoples and non-Indigenous population descriptors

‘Aboriginal and Torres Strait Islander peoples’ is the preferred descriptor used throughout the report. ‘People’ is an acceptable alternative to ‘peoples’ depending on context, but in general, the collective term ‘peoples’ is used. The ‘Indigenous Australians’ descriptor is inclusive of all Aboriginal and Torres Strait Islander groups, and is also used where space is limited.

The ‘non-Indigenous’ descriptor is used where the data collection allows for the separate identification of people who are neither Aboriginal nor Torres Strait Islander. The label ‘other Australians’ is used to refer to the combined data for non-Indigenous people, and those for whom Indigenous status was not stated.

Crude rates

A crude rate is defined as the number of events over a specified period (for example, a year) divided by the total population at risk of the event.

Age-specific rates

An age-specific rate is defined as the number of events for a specified age group over a specified period (for example, a year) divided by the total population at risk of the event in that age group. Age-specific rates in this report were calculated by dividing, for example, the number of deaths in each specified age group by the corresponding population in the same age group.

Age-standardisation

Age-standardisation controls for the effect of age, to allow comparisons of summary rates between two populations that have different age structures. Age‑standardisation is used throughout this report when comparing Aboriginal and Torres Strait Islander peoples with non-Indigenous Australians for a range of variables where age is a factor e.g. health-related measures. The main disadvantages with age-standardisation are that the resulting rates are not the real or ‘reported’ rates for the population. Age-standardised rates are therefore only meaningful as a means of comparison.

Age-standardised rates are generally derived using all age groups. However, in some cases in the Health Performance Framework report, the age-standardised rates were calculated for a particular age range in order to support study of a specific population group (for instance, the age‑standardised data for some mortality indicators were derived for the age range 0–74).
Unless otherwise specified, the direct method of age-standardisation was used – see Glossary.

^ Back to top

Rate ratio

Rate ratios are calculated by dividing the rate for Indigenous Australians with a particular characteristic by the rate for non‑Indigenous Australians with the same characteristic.

A rate ratio of 1 indicates that the prevalence/incidence of the characteristic is the same in the Indigenous and non‑Indigenous populations. Rate ratios of greater than 1 suggest higher prevalence/incidence in the Indigenous population and rate ratios of less than 1 suggest higher prevalence/incidence in the non‑Indigenous population.

Rate difference

Rate difference is calculated by subtracting the rate for Indigenous Australians from the rate for non-Indigenous Australians for the characteristic of interest.

Rounding

Decimal points on percentages and rates are rounded to whole numbers by rounding down where the decimal is less than 0.5 and up where the decimal is above 0.5. Where the decimal point is exactly 0.5, the underlying estimates are used (where available) to calculate additional decimal points to determine whether to round up or down e.g. 0.49 is rounded down.
Relative standard error
Relative standard error (RSE) is a measure of sampling error which is obtained by expressing the standard error as a percentage of the estimate. 

The ABS considers that only estimates with relative standard errors of less than 25%, and percentages based on such estimates, are sufficiently reliable for most analytical purposes. Relative standard errors between 25% and 50% should be used with caution. Estimates with relative standard errors greater than 50% are considered too unreliable for general use.

^ Back to top

Confidence intervals

The observed value of a rate may vary due to chance even where there is no variation in the underlying value of the rate. A 95% confidence interval (CI) for an estimate is a range of values which is very likely (95 times out of 100) to contain the true unknown value. CIs have not been presented for all administrative datasets as investigative work is underway into the validity of using CIs for these datasets.

Where the 95% CIs of two estimates do not overlap it can be concluded that there is a statistically significant difference between the two estimates.

As with all statistical comparisons, care should be exercised in interpreting the results of the comparison. If two rates are statistically significantly different from each other, the difference is unlikely to have arisen by chance. Judgement should, however, be exercised in deciding whether or not the difference is of any practical significance.

The standard method of calculating CIs has been used in this report. Typically, in the standard method, the observed rate is assumed to have natural variability in the numerator count (for example, deaths) but not in the population denominator count. Also, the rate is assumed to have been generated from a normal distribution (‘Bell curve’). Random variation in the numerator count is assumed to be centred around the true value; that is, there is no systematic bias.

The formulas used to calculate 95% confidence intervals using the standard method are:

Crude rate:

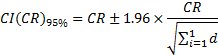
Where d = the number of deaths or other events

Age-standardised rate:

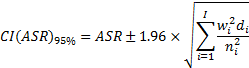
Where wi = the proportion of the standard population in age group i

di = the number of deaths or other events in age group i

ni = the number of people in the population in age group i

^ Back to top

Significance testing

Annual change and percent change were only calculated for series of 4 or more data points. The 95% confidence intervals (CIs) for the standard error of the slope estimate (annual change) based on linear regression are used to determine whether the apparent increases or decreases in the data are statistically significant at the p < 0.05 level. The formula used to calculate the CIs for the standard error of the slope estimate is:

where x is the annual change (slope estimate)

t* (n-2) is the 97.5th quantile of the tn-2 distribution.

If the upper and lower 95% confidence intervals do not include zero, then it can be concluded that there is statistical evidence of an increasing or decreasing trend in the data over the study period.

Significant changes are denoted with a * against the annual change statistics included in relevant tables.

Only sentences including data with significant differences have been used in the report. However, not all relationships in the AIHW online tables have been tested for significance (or shown with the * symbol).

Testing rate differences and rate ratios

If the 95% CIs of the difference in rates do not include zero, then it can be concluded that there is statistical evidence of a difference in rates. If the 95% CIs of the rate ratio do not include 1, then it can be concluded that there is statistical evidence of a difference in the rates contributing to the rate ratio.

Tables include a * next to the rate ratio and rate difference to indicate that rates for the Indigenous and non-Indigenous populations are statistically different from each other at the p < 0.05 level (based on 95% CIs). Where results of significance testing differed between rate ratios and rate differences, caution should be exercised in the interpretation of the tests.

^ Back to top

The word ‘significant’

Statistically significant differences, for example between jurisdictions or over time, are denoted as ‘significant’. The word ‘significant’ is not used outside its statistical context.

Significance of trends rate ratios

In the HPF, time series analyses use linear regression analysis to determine whether there have been significant increases or decreases in the observed rates. Linear regression was only used where the rate ratio trend was linear.

Annual change and per cent change

The annual change in rates and rate differences are calculated using linear regression, which uses the ‘least squares’ method to calculate a straight line that best fits the data. The simple linear regression line (Y = a + bX, or ‘slope’ estimate) was used to determine the annual change in the data over the period.

Per cent change is calculated taking the difference between the first and last points on the regression line, dividing by the first point on the line and multiplying by 100.

^ Back to top